【Java数据结构与算法】树结构应用

大顶堆和小顶堆图解说明

堆排序基本介绍

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，她也是不稳定排序。
堆是具有以下性质的完全二叉树：每个节点的值都大于或等于其左右子节点的值，称为大顶堆(注意：没有要求节点的左子节点的值和右子节点的值的大小关系)。
每个节点的值都小于或者等于其左右子节点的值，称为小顶堆。
大顶堆举例说明：

我们对堆中的节点按层进行编号，映射到数组中就是下面的样子：

大顶堆特点：arr[i]>=arr[2*i+1] && arr[i]>=arr[2*i+2] i从0开始编号，对应第几个节点。
小顶堆举例说明：

小顶堆：arr[i]<=arr[2*i+1] && arr[i] <= arr[2*i+2]; i从0开始编号，对应第几个节点。
一般升序采用大顶堆，降序采用小顶堆。

堆排序的思路图解

堆排序基本思想

将待排序序列构造成一个大顶堆(数组)。
此时，整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换，此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列。

可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了。

堆排序步骤图解说明

要求：给你一个数组{4,6,8,5,9}，要求使用堆排序法，将数组升序排序。

步骤1、构造初始堆

原始数组[4,6,8,5,9]

假设给定无序序列结构如下：
此时我们从最后一个非叶子节点开始(arr.length/2-1=5/2-1=1，也就是下面的6节点)，从左至右，从下至上进行调整。
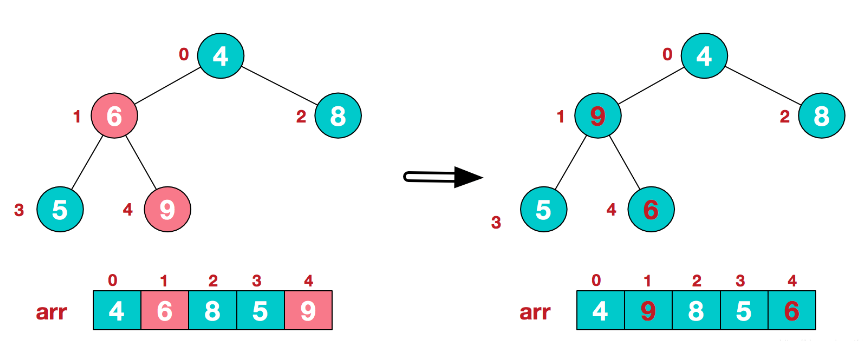
找到第二个非叶子节点4，由于[4,9,8]中9元素最大，则4和9交换。
这时，交换导致[4,5,6]结构出现混乱，继续调整，[4,5,6]中6最大，交换4和6。
此时我们就将一个无序序列构造成一个大顶堆。

步骤2、交换元素

将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

将堆顶元素 9 和末尾元素 4 进行交换。
重新调整结构，使其继续满足堆定义。
再将堆顶元素 8 与末尾元素 5 进行交换，得到第二大元素 8。
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序。

总结：

将无序序列构建成一个堆，根据升序或降序需求选择大顶堆或小顶堆。
将堆顶元素与末尾元素交换，最大元素沉到数组末端。
重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整和交换步骤，直到整个序列有序。

堆排序的代码实现

代码

package com.jokerdig.tree;

import java.util.Arrays;

/**
 * @author Joker大雄
 * @data 2022/11/4 - 11:20
 **/
// 堆排序
public class HeapSort {
    public static void main(String[] args) {
        // 要求对数组进行升序排序
        int arr[] = {4,6,8,5,9};
        System.out.println("原始数组："+ Arrays.toString(arr));
        headSort(arr);
    }
    // 编写堆排序方法
    public static void headSort(int arr[]){
        int temp = 0; // 临时变量
        System.out.println("======堆排序======");
        // 分步骤完成
        /*
        adjustHeap(arr,1,arr.length);
        System.out.println("第1次调整："+ Arrays.toString(arr));

        // 第二次调整
        adjustHeap(arr,0,arr.length);
        System.out.println("第2次调整："+ Arrays.toString(arr));
         */
        // 完整堆排序
        for (int i = arr.length/2-1; i >=0 ; i--) {
            adjustHeap(arr,i, arr.length);
        }
        for (int j = arr.length-1; j > 0; j--) {
            // 交换
            temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr,0,j); // 总是从第一个值开始调整
        }
        System.out.println("堆排序结果："+ Arrays.toString(arr));
    }
    // 将一个数组(对应二叉树)调整成一个大顶堆
    /**
     *举例：
     * 当 i=1==>{4,6,8,5,9}=>{4,9,8,5,6}
     * 当 i=0==>{4,9,8,5,6}=>{9,6,8,5,4}
     *
     * @param arr 待排序数组
     * @param i 表示非叶子节点在数组中的索引
     * @param len 数组长度，即对多少个元素进行调整
     */
    public static void adjustHeap(int arr[],int i,int len){

        int temp = arr[i]; // 先取出当前元素的值，保存在临时变量
        // 开始调整，左子节点
        for(int k = i*2+1; k<len; k=k*2+1){
            if(k+1<len && arr[k]<arr[k+1]){ // 说明左子节点的值小于右子节点的值
                k++; // k指向右子节点
            }
            if(arr[k]>temp){ // 如果子节点大于父节点
                arr[i] = arr[k]; // 把较大的值赋给当前节点
                i = k; // i指向k，继续循环比较
            }else{
                break;
            }
        }
        // 当for循环结束后，我们已经将以i为父节点的树的最大值，放在了最顶部（局部）
        arr[i] = temp; // 将temp值放到调整后的位置
    }
}

运行结果

原始数组：[4, 6, 8, 5, 9]
======堆排序======
堆排序结果：[4, 5, 6, 8, 9]

Process finished with exit code 0

经过测试 800万条随机数排序，堆排序耗费时间大约为 3s 左右；

赫夫曼树的基本介绍

基本介绍

给定n个权值作为n个叶子节点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为赫夫曼树(Huffman Tree)。
赫夫曼树是带权路径长度最短的树，权值较大的节点离根很近。

举例说明

路径和路径长度：在一棵树中，从一个节点往下可以达到的孩子或者孙子节点之间的通路，称为路径；通路中分支的数目称为路径长度。若规定根节点的层数为1，则从根节点到L层节点的路径长度为L-1。
节点的权及带权路径长度：若将树中节点赋给一个有着某种含义的数值，则这个数值称为该节点的权。节点的带权路径长度：从根节点到该节点之间的路径长度与该节点的乘积。
树的带权路径长度：树的带权路径长度规定为所有叶子节点的带权路径长度之和，记为WPL(weighted path length)，权值越大的节点离根节点越近的二叉树才是最优二叉树。
WPL最小就是赫夫曼树。

赫夫曼树创建步骤图解

给你一个数组{13,7,8,3,29,6,1}，要求转换为一颗赫夫曼树。

步骤分析：

从小到大进行排序，每个数据都是一个节点，每个几点可以看成是一棵最简单的二叉树。
取出根节点权值最小的两棵二叉树。
组成一棵新的二叉树，组成的新二叉树的根节点权值是前面两棵二叉树根节点权值的和。
再将这棵新的二叉树，以根节点的权值大小再次排序，不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树。

赫夫曼树创建代码实现

代码

package com.jokerdig.huffmanTree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

/**
 * @author Joker大雄
 * @data 2022/11/5 - 10:44
 **/
// 赫夫曼树
public class HuffmanTreeDemo {
    public static void main(String[] args) {
        int arr[] = {13,7,8,3,29,6,1};
        Node huffmanTree = createHuffmanTree(arr);
        System.out.println("========前序遍历赫夫曼树=======");
        preOrder(huffmanTree);
    }
    // 创建赫夫曼树方法
    /**
     *
     * @param arr 创建赫夫曼树的数组
     * @return 创建完毕的赫夫曼树的根节点
     */
    public static Node createHuffmanTree(int [] arr){
        /*
        1. 为了操作方便，我们遍历arr数组
        2. 将arr的每个元素构成一个Node
        3. 将Node放入到ArrayList中
         */
        List<Node> nodes = new ArrayList<Node>();
        for (int value:arr){
            nodes.add(new Node(value));
        }
        // 我们处理的过程是循环进行的
        // 当集合中只剩最后一个节点，循环退出，赫夫曼殊构建完成
        while(nodes.size()>1){

            // 排序,从小到大
            Collections.sort(nodes);
            // System.out.println("nodes"+nodes);

            // 取出根节点权值最小的两个二叉树
            // 1. 取出权值最小的节点
            Node leftNode = nodes.get(0);
            // 2. 取出权值第二小的节点
            Node rightNode  = nodes.get(1);
            // 3. 构建一棵新的二叉树
            Node parent = new Node(leftNode .value+rightNode .value);
            parent.left = leftNode;
            parent.right = rightNode;
            // ArrayList中删除处理过的节点
            nodes.remove(leftNode);
            nodes.remove(rightNode);
            // 将新的二叉树加入到nodes中
            nodes.add(parent);
        }
        // 返回root节点
        return nodes.get(0);
    }
    // 前序遍历
    public static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("该赫夫曼树为空");
        }
    }
}
// 创建节点
// 为了让Node对象持续排序，需要使用Collections集合斤西瓜内排序
// 让Node实现Comparable接口
class Node implements Comparable<Node>{
    int value; // 节点权值
    Node left; // 指向左子节点
    Node right;// 指向右子节点

    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }
    // Comparable接口方法
    @Override
    public int compareTo(Node o) {
        // 表示从小到大进行排序
        // 返回值大于0，this.value>o.value
        // 返回值小于0，this.value<o.value
        return this.value-o.value;
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

========前序遍历赫夫曼树=======
Node{value=67}
Node{value=29}
Node{value=38}
Node{value=15}
Node{value=7}
Node{value=8}
Node{value=23}
Node{value=10}
Node{value=4}
Node{value=1}
Node{value=3}
Node{value=6}
Node{value=13}

Process finished with exit code 0

赫夫曼编码介绍及变长编码举例

基本介绍

赫夫曼编码也翻译为哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，属于一种程序算法。
赫夫曼编码是赫夫曼树在电讯通信中的经典应用之一。
赫夫曼便阿门广泛地用于数据文件压缩。其压缩率通常在20%~90%之间。
赫夫曼码是可变字长编码(VLC)的一种，由Huffman于1952年提出的一种编码方式，也称为最佳编码。

原理剖析

在通信领域中信息的处理方式

定长编码
- java javascript spring mybatis // 共30个字符(包括空格)
- 106 97 118 97 32 106 97 118 97 115 99 114 105 112 116 32 115 112 114 105 110 103 32 109 121 98 97 116 105 115 // 对应Ascii码(十进制)
- 01101010 01100001 01110110 01100001 00100000 01101010 01100001 01110110 01100001 01110011 01100011 01110010 01101001 01110000 01110100 00100000 01110011 01110000 01110010 01101001 01101110 01100111 00100000 01101101 01111001 01100010 01100001 01110100 01101001 01110011 // 对应二进制
- 按照二进制来传递信息，总长度为319(包括空格)
- 在线转码网站：https://www.rapidtables.org/zh-CN/convert/number/ascii-hex-bin-dec-converter.html
变长编码
- java javascript spring mybatis // 共30个字符(包括空格)
- c:1 n:1 g:1 m:1 y:1 b:1 j:2 v:2 r:2 p:2 t:2 s:3 i:3 :3 a:5 // 各个字符对应的个数
- 0=a,1= ,10=i,11=s,100=t,101=p,110=r,111=v,1000=j,1001=b,1010=y,1011=m,1100=g,1101=n,1110=c
  
  说明：按照各个字符出现的次数进行编码，原则是出现次数越多，则编码越小；
- 按照上面给的各个字符规定的编码，在传输"java javascript spring mybatis"时，编码为：
  
  1000011101100001110111110110101011001111011101011011100110111010100101001011
- 字符的编码都不能是其它字符编码的前缀，符合此要求的编码叫做前缀编码，即不能匹配到重复的编码；（我们上面的这种方式不符合前缀编码的要求，在解码时可能会出现混乱）

赫夫曼编码的原理图解

赫夫曼编码

java javascript spring mybatis // 共30个字符(包括空格)
c:1 n:1 g:1 m:1 y:1 b:1 j:2 v:2 r:2 p:2 t:2 s:3 i:3 :3 a:5 // 统计各个字符出现的次数

按照上面字符出现的次数构建一棵赫夫曼树，次数作为权值
分析图解：
- 我们规定向左为0，向右为1进行编码；
  
  这时候编码分别为：
  
  c:10000 n:10001 g:01110 m:01111
  
  y:01100 b:01101 j:1001 v:1010
  
  r:1011 p:1100 t:1101
  
  s:000 i:001 :010 a:111
  
  我们发现该编码属于前缀编码，每一个编码之间不会冲突；
- 按照上面给的各个字符规定的编码，在传输"java javascript spring mybatis"时，编码为：
  
  1001111101011101010011111010111000100001011001110011010010001100101100110001011100100111101100011011111101001000 // 长度为112
- 长度由原来的319压缩至112，压缩率为：(319-112)/319=61.8% (无损压缩)

注意事项

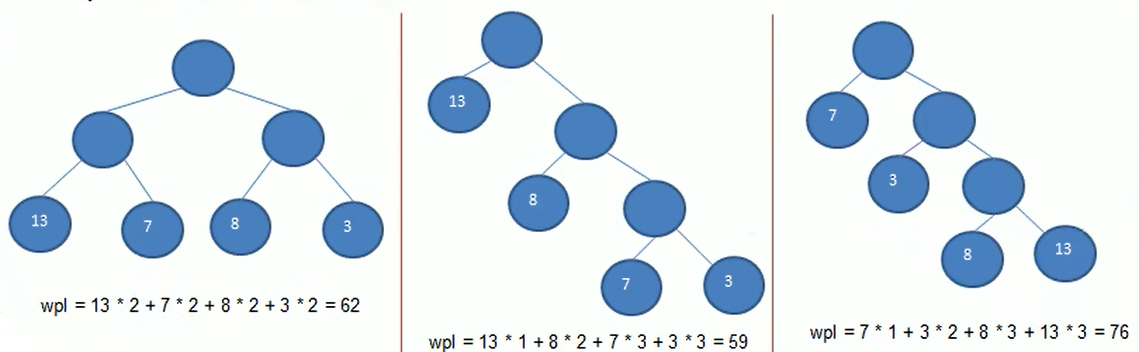
赫夫曼树的根据排序方法的不同，也可能会不太一样，这样对应的赫夫曼编码也完全不一样，但wpl是一样的，都是最小的。

例如：在排序时发现多个权值是相等的，那么在构建过程中相等权值，存放顺序不同，也会导致所构建的赫夫曼树不同。

数据压缩-创建赫夫曼树思路

给出一段文本，比如"java javascript spring mybatis"，根据前面的赫夫曼编码原理，对其进行数据压缩处理。

根据赫夫曼编码压缩数据的原理，需要创建"java javascript spring mybatis"对应的赫夫曼树。

步骤分析：

Node{data{存放数据} ，weight{权值}，left和right}。
得到"java javascript spring mybatis"对应的byte[]数组。
编写一个方法，将准备构建赫夫曼树的Node节点放到List，例如[Node[data=32,weight=3]…]。
可以通过List创建对应的赫夫曼树。

数据压缩-创建赫夫曼树实现

代码

package com.jokerdig.huffmanCode;

import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/8 - 15:12
 **/
public class HuffmanCode {
    public static void main(String[] args) {
        String str = "java javascript spring mybatis";
        byte[] contentBytes = str.getBytes();
        List<Node> nodes = getNodes(contentBytes);
        // 测试赫夫曼树
        System.out.println("======创建的赫夫曼树====");
        Node huffmanTree = createHuffmanTree(nodes);
        // 前序遍历赫夫曼树
        huffmanTree.preOrder();
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }
    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

======创建的赫夫曼树======
Node{data=null, weight=30}
Node{data=null, weight=13}
Node{data=null, weight=6}
Node{data=32, weight=3}
Node{data=105, weight=3}
Node{data=null, weight=7}
Node{data=115, weight=3}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=112, weight=2}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=null, weight=4}
Node{data=114, weight=2}
Node{data=116, weight=2}
Node{data=null, weight=4}
Node{data=118, weight=2}
Node{data=null, weight=2}
Node{data=98, weight=1}
Node{data=99, weight=1}
Node{data=null, weight=9}
Node{data=null, weight=4}
Node{data=null, weight=2}
Node{data=103, weight=1}
Node{data=109, weight=1}
Node{data=null, weight=2}
Node{data=110, weight=1}
Node{data=121, weight=1}
Node{data=97, weight=5}


Process finished with exit code 0

数据压缩-生成赫夫曼编码表

思路分析

我们已经生成了赫夫曼树，继续完成任务：

生成赫夫曼树对应的赫夫曼编码，如：32=000, 97=111, 98=10110, 99=10111, 103=11000, 105=001, 106=0110, 109=11001, 110=11010, 112=0111, 114=1000, 115=010, 116=1001, 118=1010, 121=11011；
使用赫夫曼编码来生成赫夫曼编码数据，即按照上方的赫夫曼编码，将"java javascript spring mybatis"字符串生成对应的编码数据，形式如下：1001111101011101010011111010111000100001011001110011010010001100101100110001011100100111101100011011111101001000；

代码实现

代码

package com.jokerdig.huffmanCode;

import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/8 - 15:12
 **/
public class HuffmanCode {
    public static void main(String[] args) {
        String str = "java javascript spring mybatis";
        byte[] contentBytes = str.getBytes();
        // System.out.println("初始长度："+contentBytes.length);
        List<Node> nodes = getNodes(contentBytes);
        // 测试赫夫曼树
        System.out.println("======创建的赫夫曼树======");
        Node huffmanTree = createHuffmanTree(nodes);
        // 前序遍历赫夫曼树
        huffmanTree.preOrder();
        // 测试生成对应的赫夫曼编码
        getCodes(huffmanTree);
        System.out.println("======生成的赫夫曼编码表======");
        System.out.println(huffmanCodes);
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node,String code,StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

======创建的赫夫曼树======
Node{data=null, weight=30}
Node{data=null, weight=13}
Node{data=null, weight=6}
Node{data=32, weight=3}
Node{data=105, weight=3}
Node{data=null, weight=7}
Node{data=115, weight=3}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=112, weight=2}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=null, weight=4}
Node{data=114, weight=2}
Node{data=116, weight=2}
Node{data=null, weight=4}
Node{data=118, weight=2}
Node{data=null, weight=2}
Node{data=98, weight=1}
Node{data=99, weight=1}
Node{data=null, weight=9}
Node{data=null, weight=4}
Node{data=null, weight=2}
Node{data=103, weight=1}
Node{data=109, weight=1}
Node{data=null, weight=2}
Node{data=110, weight=1}
Node{data=121, weight=1}
Node{data=97, weight=5}
======生成的赫夫曼编码表======
{32=000, 97=111, 98=10110, 99=10111, 103=11000, 105=001, 106=0110, 109=11001, 110=11010, 112=0111, 114=1000, 115=010, 116=1001, 118=1010, 121=11011}

Process finished with exit code 0

数据压缩-赫夫曼编码字节数组

代码

package com.jokerdig.huffmanCode;

import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/8 - 15:12
 **/
public class HuffmanCode {
    public static void main(String[] args) {
        String str = "java javascript spring mybatis";
        byte[] contentBytes = str.getBytes();
        // System.out.println("初始长度："+contentBytes.length);
        List<Node> nodes = getNodes(contentBytes);
        // 测试赫夫曼树
        System.out.println("======创建的赫夫曼树======");
        Node huffmanTree = createHuffmanTree(nodes);
        // 前序遍历赫夫曼树
        huffmanTree.preOrder();
        // 测试生成对应的赫夫曼编码
        getCodes(huffmanTree);
        System.out.println("======生成的赫夫曼编码表======");
        System.out.println(huffmanCodes);

        // 测试
        byte[] huffmanCodeByte = zipData(contentBytes,huffmanCodes);
        System.out.println("======通过赫夫曼编码表压缩数据=======");
        System.out.println(Arrays.toString(huffmanCodeByte));
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }

   // 编写一个方法，将字符串对应的byte[]数组，通过生成的赫夫曼编码表进行处理，返回处理过后的字节数组
    static StringBuilder huffmanStr = new StringBuilder();//存储赫夫曼编码对应的字符串，在解码的时候使用
    /**
     *
     * @param bytes 原始字符串对应的byte数组
     * @param huffmanCodes 生成的赫夫曼编码
     * @return 返回处理后的byte数组，8位为一组
     * huffmanCodeBytes[0] = 10011111(补码) =>10011111-1 => 10011110(反码)=>11100001(原码)
     */
    private static byte[] zipData(byte[] bytes,Map<Byte,String> huffmanCodes){

        // 1. 利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 遍历bytes数组
        for (byte b:bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
        huffmanStr = stringBuilder; // 记录赫夫曼编码对应字符串
        // 字符串转成byte数组
        // 统计返回的byte[] huffmanCodeBytes长度
        // 一句代码写法： int len = (stringBuilder.length()+7)/8;
        int len;
        if(stringBuilder.length()%8==0){// 是整数
            len = stringBuilder.length()/8;
        }else{
            len = stringBuilder.length()/8+1;
        }
        // 创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0;// 记录byte次数
        for (int i = 0; i < stringBuilder.length(); i+=8) {// 步长为8
            String strByte;
            if(i+8>stringBuilder.length()){
                // 长度不够8位
                strByte = stringBuilder.substring(i);
            }else{
                // 每次取8位
                strByte = stringBuilder.substring(i,i+8);
            }
            // 将strByte，转成byte数组，放入huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2); // radix 进制
            index++;
        }
        return huffmanCodeBytes;
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node,String code,StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

======创建的赫夫曼树======
Node{data=null, weight=30}
Node{data=null, weight=13}
Node{data=null, weight=6}
Node{data=32, weight=3}
Node{data=105, weight=3}
Node{data=null, weight=7}
Node{data=115, weight=3}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=112, weight=2}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=null, weight=4}
Node{data=114, weight=2}
Node{data=116, weight=2}
Node{data=null, weight=4}
Node{data=118, weight=2}
Node{data=null, weight=2}
Node{data=98, weight=1}
Node{data=99, weight=1}
Node{data=null, weight=9}
Node{data=null, weight=4}
Node{data=null, weight=2}
Node{data=103, weight=1}
Node{data=109, weight=1}
Node{data=null, weight=2}
Node{data=110, weight=1}
Node{data=121, weight=1}
Node{data=97, weight=5}
======生成的赫夫曼编码表======
{32=000, 97=111, 98=10110, 99=10111, 103=11000, 105=001, 106=0110, 109=11001, 110=11010, 112=0111, 114=1000, 115=010, 116=1001, 118=1010, 121=11011}
======通过赫夫曼编码表压缩数据=======
[111, 92, 55, -82, -81, 5, -28, 39, -125, -84, 12, -18, -34, 74]

Process finished with exit code 0

数据压缩-赫夫曼字节数组封装

代码

package com.jokerdig.huffmanCode;

import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/8 - 15:12
 **/
public class HuffmanCode {
    public static void main(String[] args) {
        String str = "java javascript spring mybatis";
        byte[] contentBytes = str.getBytes();
        byte[] huffmanCodeByte = huffmanZip(contentBytes);
        System.out.println("======通过赫夫曼编码表压缩数据=======");
        System.out.println(Arrays.toString(huffmanCodeByte));
    }
    // 编写一个方法，封装下面的所有方便调用
    /**
     *
     * @param bytes 原始字符串对应的数组
     * @return  经过赫夫曼编码处理后的数组
     */
    private static byte[] huffmanZip(byte[] bytes){
        List<Node> nodes = getNodes(bytes);
        // 根据nodes创建赫夫曼树
        Node huffmanTree = createHuffmanTree(nodes);
        // 生成对应的赫夫曼编码
        Map<Byte,String> huffmanCodes = getCodes(huffmanTree);
        // 根据赫夫曼编码表压缩数据
        byte[] huffmanCodeByte = zipData(bytes,huffmanCodes);
        return huffmanCodeByte;
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }

    // 编写一个方法，将字符串对应的byte[]数组，通过生成的赫夫曼编码表进行处理，返回处理过后的字节数组
    static StringBuilder huffmanStr = new StringBuilder();//存储赫夫曼编码对应的字符串，在解码的时候使用
    /**
     *
     * @param bytes 原始字符串对应的byte数组
     * @param huffmanCodes 生成的赫夫曼编码
     * @return 返回处理后的byte数组，8位为一组
     * huffmanCodeBytes[0] = 10011111(补码) =>10011111-1 => 10011110(反码)=>11100001(原码)
     */
    private static byte[] zipData(byte[] bytes,Map<Byte,String> huffmanCodes){

        // 1. 利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 遍历bytes数组
        for (byte b:bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
        huffmanStr = stringBuilder; // 记录赫夫曼编码对应字符串
        // 字符串转成byte数组
        // 统计返回的byte[] huffmanCodeBytes长度
        // 一句代码写法： int len = (stringBuilder.length()+7)/8;
        int len;
        if(stringBuilder.length()%8==0){// 是整数
            len = stringBuilder.length()/8;
        }else{
            len = stringBuilder.length()/8+1;
        }
        // 创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0;// 记录byte次数
        for (int i = 0; i < stringBuilder.length(); i+=8) {// 步长为8
            String strByte;
            if(i+8>stringBuilder.length()){
                // 长度不够8位
                strByte = stringBuilder.substring(i);
            }else{
                // 每次取8位
                strByte = stringBuilder.substring(i,i+8);
            }
            // 将strByte，转成byte数组，放入huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2); // radix 进制
            index++;
        }
        return huffmanCodeBytes;
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node,String code,StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

======通过赫夫曼编码表压缩数据=======
[111, 92, 55, -82, -81, 5, -28, 39, -125, -84, 12, -18, -34, 74]

Process finished with exit code 0

数据解压-字节转二进制字符串

思路分析

使用赫夫曼编码来解码数据，具体要求如下：

之前我们得到了赫夫曼编码和对应的编码数组byte[]，即[111, 92, 55, -82, -81, 5, -28, 39, -125, -84, 12, -18, -34, 74]；
现在要求使用赫夫曼编码，进行解码，又重新得到原来的字符串"java javascript spring mybatis"；

代码实现

代码

// 1. 先将huffmanCodeBytes数组重新转为赫夫曼编码对应二进制字符串
/**
     *
     * @param flag 标识是否需要补高位
     * @param bt 传入的字节
     * @return 返回对应二进制字符串
     */
private static String byteToBitString(boolean flag,byte bt){
    // 使用变量保存bt
    int temp = bt; // 将bt转为int
    if(flag){
        // 如果传入的是正数，还存在补高位的问题
        temp |= 256; // temp=1 ->100000001
    }
    String str = Integer.toBinaryString(temp);
    if(flag){
        return str.substring(str.length()-8); // 这里返回的temp对应的二进制的补码
    }else{
        return str;
    }
}

数据解压-赫夫曼解码

代码

package com.jokerdig.huffmanCode;

import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/8 - 15:12
 **/
public class HuffmanCode {
    public static void main(String[] args) {
        String str = "java javascript spring mybatis";
        byte[] contentBytes = str.getBytes();
        byte[] huffmanCodeByte = huffmanZip(contentBytes);
        System.out.println("======通过赫夫曼编码表压缩数据=======");
        System.out.println(Arrays.toString(huffmanCodeByte));
        // 测试解码
        System.out.println("======解压后的数据======");
        byte[] source = decode(huffmanCodes, huffmanCodeByte);
        System.out.println(new String(source));
    }
    // 完成数据解压
    // 1. 先将huffmanCodeBytes数组重新转为赫夫曼编码对应二进制字符串
    /**
     *
     * @param flag 标识是否需要补高位，如果是最后一个字节，不需要补高位
     * @param bt 传入的字节
     * @return 返回对应二进制字符串
     */
    private static String byteToBitString(boolean flag,byte bt){
        // 使用变量保存bt
        int temp = bt; // 将bt转为int
        if(flag){
            // 如果传入的是正数，还存在补高位的问题
            temp |= 256; // temp=1 ->100000001
        }
        String str = Integer.toBinaryString(temp);
        if(flag){
            return str.substring(str.length()-8); // 这里返回的temp对应的二进制的补码
        }else{
            return str;
        }
    }
    // 2. 将赫夫曼编码对应的二进制字符串对照赫夫曼编码转为原本的字符串

    /**
     *
     * @param huffmanCodes 赫夫曼编码
     * @param huffmanBytes 赫夫曼编码处理过的数组
     * @return 解码后的字符串对应的数组
     */
    private static byte[] decode(Map<Byte,String> huffmanCodes,byte[] huffmanBytes){
        // 先得到huffmanBytes对应的二进制的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 将byte数组转称二进制的字符串
        for (int i = 0; i < huffmanBytes.length-1; i++) {
            stringBuilder.append(byteToBitString(true,huffmanBytes[i]));
        }
        // 字节数组的最后一个字节另做处理，如果是负数，flag为true；
        // 如果是正数，flag为false，拼接后长度与原先相等不做处理，若小于原先长度则先补0后拼接，使其与原先长度相等
        if(huffmanBytes[huffmanBytes.length-1]<0){
            stringBuilder.append(byteToBitString(true,huffmanBytes[huffmanBytes.length-1]));
        }else{
            String str = byteToBitString(false,huffmanBytes[huffmanBytes.length-1]);
            while(str.length()+stringBuilder.length()<huffmanStr.length()){
                // 补位
                stringBuilder.append(0);
            }
            stringBuilder.append(str);
        }

        // 把字符串按照指定的赫夫曼编码进行解码
        // 把赫夫曼编码表进行调换，来反向查询
        Map<String,Byte> map = new HashMap<String,Byte>();
        for (Map.Entry<Byte,String> entry:huffmanCodes.entrySet()){
            // 反向存放
            map.put(entry.getValue(),entry.getKey());
        }

        // 创建集合，存放byte
        List<Byte> byteList = new ArrayList<>();
        // i是索引，扫描stringBuilder
        for(int i = 0;i<stringBuilder.length();){
            int count = 1; // 计数器
            Byte b = null;
            boolean flag = true;
            while(flag){
                String key = stringBuilder.substring(i,i+count);
                b = map.get(key);
                if(b==null){ // 说明没有匹配到
                    count++;
                }else{
                    flag = false;
                }
            }
            byteList.add(b);
            i+=count; // 把i移动到count
        }
        // 把byteList中的输入放入到byte[]数组并返回
        byte[] bts = new byte[byteList.size()];
        for (int i = 0; i < bts.length; i++) {
            bts[i] = byteList.get(i);
        }
        return bts;
    }
    // 编写一个方法，封装下面的所有方便调用
    /**
     *
     * @param bytes 原始字符串对应的数组
     * @return  经过赫夫曼编码处理后的数组
     */
    private static byte[] huffmanZip(byte[] bytes){
        List<Node> nodes = getNodes(bytes);
        // 根据nodes创建赫夫曼树
        Node huffmanTree = createHuffmanTree(nodes);
        // 生成对应的赫夫曼编码
        Map<Byte,String> huffmanCodes = getCodes(huffmanTree);
        // 根据赫夫曼编码表压缩数据
        byte[] huffmanCodeByte = zipData(bytes,huffmanCodes);
        return huffmanCodeByte;
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }

    // 编写一个方法，将字符串对应的byte[]数组，通过生成的赫夫曼编码表进行处理，返回处理过后的字节数组
    static StringBuilder huffmanStr = new StringBuilder();//存储赫夫曼编码对应的字符串，在解码的时候使用
    /**
     *
     * @param bytes 原始字符串对应的byte数组
     * @param huffmanCodes 生成的赫夫曼编码
     * @return 返回处理后的byte数组，8位为一组
     * huffmanCodeBytes[0] = 10011111(补码) =>10011111-1 => 10011110(反码)=>11100001(原码)
     */
    private static byte[] zipData(byte[] bytes,Map<Byte,String> huffmanCodes){

        // 1. 利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 遍历bytes数组
        for (byte b:bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
        huffmanStr = stringBuilder; // 记录赫夫曼编码对应字符串
        // 字符串转成byte数组
        // 统计返回的byte[] huffmanCodeBytes长度
        // 一句代码写法： int len = (stringBuilder.length()+7)/8;
        int len;
        if(stringBuilder.length()%8==0){// 是整数
            len = stringBuilder.length()/8;
        }else{
            len = stringBuilder.length()/8+1;
        }
        // 创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0;// 记录byte次数
        for (int i = 0; i < stringBuilder.length(); i+=8) {// 步长为8
            String strByte;
            if(i+8>stringBuilder.length()){
                // 长度不够8位
                strByte = stringBuilder.substring(i);
            }else{
                // 每次取8位
                strByte = stringBuilder.substring(i,i+8);
            }
            // 将strByte，转成byte数组，放入huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2); // radix 进制
            index++;
        }
        return huffmanCodeBytes;
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node,String code,StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

======通过赫夫曼编码表压缩数据=======
[111, 92, 55, -82, -81, 5, -28, 39, -125, -84, 12, -18, -34, 74]
======解压后的数据======
java javascript spring mybatis

Process finished with exit code 0

使用赫夫曼编码压缩文件

思路分析

我们来完成对文件的压缩和解压，要求：给你一个图片文件，要求对其进行无损压缩，并查看压缩效果。

思路：读取文件->得到赫夫曼编码表->完成压缩

代码实现

在D盘存放一张zip.png的图片，初始大小为216KB，压缩后大小为94KB

代码

package com.jokerdig.huffmanCodeZip;

import java.io.FileInputStream;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectOutputStream;
import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/11 - 10:23
 **/
public class HuffmanCodeZip {
    public static void main(String[] args) {
        // 测试压缩图片文件
        String srcFile = "D:/zip.png";
        String dsFile = "D:/zipImage.zip";
        zipFile(srcFile,dsFile);
        System.out.println("文件压缩完毕！");

    }

    // 编写方法，将一个文件进行压缩
    /**
     *
     * @param srcFile 源文件完整路径
     * @param dsFile 压缩后的文件存放路径
     */
    public static void zipFile(String srcFile,String dsFile){
        // 创建文件输入流
        FileInputStream fileInput = null;
        // 创建文件输出流
        FileOutputStream fileOutput = null;
        // 创建ObjectOutput
        ObjectOutputStream objectOutput = null;
        try {
            fileInput = new FileInputStream(srcFile);
            // 创建一个和源文件大小一样的byte[]数组
            byte[] bt = new byte[fileInput.available()];
            // 读取图片文件
            fileInput.read(bt);
            // 获取文件对应的赫夫曼编码表
            byte[] huffmanBytes= huffmanZip(bt);
            // 创建文件的输出流，存放压缩文件
            fileOutput = new FileOutputStream(dsFile);
            // 创建一个和文件输出流关联的ObjectOutputStream
            objectOutput = new ObjectOutputStream(fileOutput);
            // 把赫夫曼便编码处理后的字节数组写入压缩文件
            objectOutput.writeObject(huffmanBytes);
            // 对象流的方式写入赫夫曼编码，为了恢复文件时使用
            objectOutput.writeObject(huffmanCodes);

        } catch (Exception e) {
            System.out.println(e.getMessage());
        }finally{
            try {
                // 关闭流
                objectOutput.close();
                fileOutput.close();
                fileInput.close();

            } catch (IOException e) {
                System.out.println(e.getMessage());
            }
        }
    }

    // 编写一个方法，封装下面的所有方便调用
    /**
     *
     * @param bytes 原始字符串对应的数组
     * @return  经过赫夫曼编码处理后的数组
     */
    private static byte[] huffmanZip(byte[] bytes){
        List<Node> nodes = getNodes(bytes);
        // 根据nodes创建赫夫曼树
        Node huffmanTree = createHuffmanTree(nodes);
        // 生成对应的赫夫曼编码
        Map<Byte,String> huffmanCodes = getCodes(huffmanTree);
        // 根据赫夫曼编码表压缩数据
        byte[] huffmanCodeByte = zipData(bytes,huffmanCodes);
        return huffmanCodeByte;
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();
        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }

    // 编写一个方法，将字符串对应的byte[]数组，通过生成的赫夫曼编码表进行处理，返回处理过后的字节数组
    static StringBuilder huffmanStr = new StringBuilder();//存储赫夫曼编码对应的字符串，在解码的时候使用
    /**
     *
     * @param bytes 原始字符串对应的byte数组
     * @param huffmanCodes 生成的赫夫曼编码
     * @return 返回处理后的byte数组，8位为一组
     * huffmanCodeBytes[0] = 10011111(补码) =>10011111-1 => 10011110(反码)=>11100001(原码)
     */
    private static byte[] zipData(byte[] bytes,Map<Byte,String> huffmanCodes){

        // 1. 利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 遍历bytes数组
        for (byte b:bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
        huffmanStr = stringBuilder; // 记录赫夫曼编码对应字符串
        // 字符串转成byte数组
        // 统计返回的byte[] huffmanCodeBytes长度
        // 一句代码写法： int len = (stringBuilder.length()+7)/8;
        int len;
        if(stringBuilder.length()%8==0){// 是整数
            len = stringBuilder.length()/8;
        }else{
            len = stringBuilder.length()/8+1;
        }
        // 创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0;// 记录byte次数
        for (int i = 0; i < stringBuilder.length(); i+=8) {// 步长为8
            String strByte;
            if(i+8>stringBuilder.length()){
                // 长度不够8位
                strByte = stringBuilder.substring(i);
            }else{
                // 每次取8位
                strByte = stringBuilder.substring(i,i+8);
            }
            // 将strByte，转成byte数组，放入huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2); // radix 进制
            index++;
        }
        return huffmanCodeBytes;
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node, String code, StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

1
2
3

文件压缩完毕！

Process finished with exit code 0

注意：如果你压缩图片后出现大小没变或者压缩后比压缩前还大的问题，可以查看注意事项部分。

使用赫夫曼编码解压文件

思路分析

要求：将之前压缩的文件，重新恢复为原来的文件。

思路：读取压缩文件->完成解压(恢复)

代码实现

代码

package com.jokerdig.huffmanCodeZip;

import java.io.*;
import java.util.*;

/**
 * @author Joker大雄
 * @data 2022/11/11 - 10:23
 **/
public class HuffmanCodeZip {
    public static void main(String[] args) {
        // 测试压缩图片文件
        String srcFile = "D:/zip.png";
        String dsFile = "D:/zipImage.zip";
        zipFile(srcFile,dsFile);
        System.out.println("文件压缩完毕！");
        // 测试解压文件
        String unZip = "D:/unZip.png";
        unZipFile(dsFile,unZip);
        System.out.println("文件解压完毕！");
    }
    // 编写方法，将文件进行解压
    /**
     *
     * @param zipFile 准备解压的文件
     * @param dsFile  解压后文件的路径
     */
    public static void unZipFile(String zipFile,String dsFile){
        // 创建文件输入流
        InputStream input = null;
        // 创建对象输入流
        ObjectInputStream objectInput = null;
        // 创建文件输出流
        OutputStream output = null;

        // 创建文件输入流
        try {
            input = new FileInputStream(zipFile);
            // 创建和input关联的对象输入流
            objectInput = new ObjectInputStream(input);
            // 读取huffmanBytes数组
            byte[] huffmanBytes = (byte[]) objectInput.readObject();
            // 读取赫夫曼编码表
            Map<Byte,String> huffmanCodes =(Map<Byte,String>) objectInput.readObject();
            // 解码
            byte[] bytes = decode(huffmanCodes, huffmanBytes);
            // 将解码后的byte数组写入到目标文件
            output = new FileOutputStream(dsFile);
            // 写出数据
            output.write(bytes);
        } catch (Exception e) {
            System.out.println(e.getMessage());
        }finally{
            // 关闭流
            try {
                output.close();
                objectInput.close();
                input.close();
            } catch (IOException e) {
                System.out.println(e.getMessage());
            }
        }
    }
    // 编写方法，将一个文件进行压缩
    /**
     *
     * @param srcFile 源文件完整路径
     * @param dsFile 压缩后的文件存放路径
     */
    public static void zipFile(String srcFile,String dsFile){
        // 创建文件输入流
        FileInputStream fileInput = null;
        // 创建文件输出流
        FileOutputStream fileOutput = null;
        // 创建ObjectOutput
        ObjectOutputStream objectOutput = null;
        try {
            fileInput = new FileInputStream(srcFile);
            // 创建一个和源文件大小一样的byte[]数组
            byte[] bt = new byte[fileInput.available()];
            // 读取图片文件
            fileInput.read(bt);
            // 获取文件对应的赫夫曼编码表
            byte[] huffmanBytes= huffmanZip(bt);
            // 创建文件的输出流，存放压缩文件
            fileOutput = new FileOutputStream(dsFile);
            // 创建一个和文件输出流关联的ObjectOutputStream
            objectOutput = new ObjectOutputStream(fileOutput);
            // 把赫夫曼便编码处理后的字节数组写入压缩文件
            objectOutput.writeObject(huffmanBytes);
            // 对象流的方式写入赫夫曼编码，为了恢复文件时使用
            objectOutput.writeObject(huffmanCodes);

        } catch (Exception e) {
            System.out.println(e.getMessage());
        }finally{
            try {
                // 关闭流
                objectOutput.close();
                fileOutput.close();
                fileInput.close();

            } catch (IOException e) {
                System.out.println(e.getMessage());
            }
        }
    }
    // 完成数据解压
    // 1. 先将huffmanCodeBytes数组重新转为赫夫曼编码对应二进制字符串
    /**
     *
     * @param flag 标识是否需要补高位，如果是最后一个字节，不需要补高位
     * @param bt 传入的字节
     * @return 返回对应二进制字符串
     */
    private static String byteToBitString(boolean flag,byte bt){
        // 使用变量保存bt
        int temp = bt; // 将bt转为int
        if(flag){
            // 如果传入的是正数，还存在补高位的问题
            temp |= 256; // temp=1 ->100000001
        }
        String str = Integer.toBinaryString(temp);
        if(flag){
            return str.substring(str.length()-8); // 这里返回的temp对应的二进制的补码
        }else{
            return str;
        }
    }
    // 2. 将赫夫曼编码对应的二进制字符串对照赫夫曼编码转为原本的字符串

    /**
     *
     * @param huffmanCodes 赫夫曼编码
     * @param huffmanBytes 赫夫曼编码处理过的数组
     * @return 解码后的字符串对应的数组
     */
    private static byte[] decode(Map<Byte,String> huffmanCodes,byte[] huffmanBytes){
        // 先得到huffmanBytes对应的二进制的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 将byte数组转称二进制的字符串
        for (int i = 0; i < huffmanBytes.length-1; i++) {
            stringBuilder.append(byteToBitString(true,huffmanBytes[i]));
        }
        // 字节数组的最后一个字节另做处理，如果是负数，flag为true；
        // 如果是正数，flag为false，拼接后长度与原先相等不做处理，若小于原先长度则先补0后拼接，使其与原先长度相等
        if(huffmanBytes[huffmanBytes.length-1]<0){
            stringBuilder.append(byteToBitString(true,huffmanBytes[huffmanBytes.length-1]));
        }else{
            String str = byteToBitString(false,huffmanBytes[huffmanBytes.length-1]);
            while(str.length()+stringBuilder.length()<huffmanStr.length()){
                // 补位
                stringBuilder.append(0);
            }
            stringBuilder.append(str);
        }

        // 把字符串按照指定的赫夫曼编码进行解码
        // 把赫夫曼编码表进行调换，来反向查询
        Map<String,Byte> map = new HashMap<String,Byte>();
        for (Map.Entry<Byte,String> entry:huffmanCodes.entrySet()){
            // 反向存放
            map.put(entry.getValue(),entry.getKey());
        }

        // 创建集合，存放byte
        List<Byte> byteList = new ArrayList<>();
        // i是索引，扫描stringBuilder
        for(int i = 0;i<stringBuilder.length();){
            int count = 1; // 计数器
            Byte b = null;
            boolean flag = true;
            while(flag){
                String key = stringBuilder.substring(i,i+count);
                b = map.get(key);
                if(b==null){ // 说明没有匹配到
                    count++;
                }else{
                    flag = false;
                }
            }
            byteList.add(b);
            i+=count; // 把i移动到count
        }
        // 把byteList中的输入放入到byte[]数组并返回
        byte[] bts = new byte[byteList.size()];
        for (int i = 0; i < bts.length; i++) {
            bts[i] = byteList.get(i);
        }
        return bts;
    }
    // 编写一个方法，封装下面的所有方便调用
    /**
     *
     * @param bytes 原始字符串对应的数组
     * @return  经过赫夫曼编码处理后的数组
     */
    private static byte[] huffmanZip(byte[] bytes){
        List<Node> nodes = getNodes(bytes);
        // 根据nodes创建赫夫曼树
        Node huffmanTree = createHuffmanTree(nodes);
        // 生成对应的赫夫曼编码
        Map<Byte,String> huffmanCodes = getCodes(huffmanTree);
        // 根据赫夫曼编码表压缩数据
        byte[] huffmanCodeByte = zipData(bytes,huffmanCodes);
        return huffmanCodeByte;
    }
    /***
     *
     * @param bytes 接收字节数组
     * @return 返回值
     */
    private static List<Node> getNodes(byte[] bytes){
        // 创建ArrayList
        List<Node> nodeList = new ArrayList<Node>();

        // 存储每个byte出现的次数 -> map
        Map<Byte,Integer> counts = new HashMap<>();
        for(byte b:bytes){
            Integer count = counts.get(b);
            if(count==null){
                // Map还没有字符数据
                counts.put(b,1);
            }else{
                counts.put(b,count+1);
            }
        }

        // 把每个键值对转换为一个Node对象，并加入到Nodes集合
        // 遍历Map并把键值对放到Node中
        for(Map.Entry<Byte,Integer> entry:counts.entrySet()){
            nodeList.add(new Node(entry.getKey(),entry.getValue()));
        }
        return nodeList;
    }

    // 通过NodeList创建对应的赫夫曼树
    private static Node createHuffmanTree(List<Node> node){
        while(node.size()>1){
            // 排序 从小到大
            Collections.sort(node);
            // 取出前两棵最小二叉树
            Node leftNode = node.get(0);
            Node rightNode = node.get(1);
            // 创建一棵新的二叉树，根节点没有data，只有权值
            Node parent = new Node(null,leftNode.weight+rightNode.weight);
            parent.left = leftNode;
            parent.right = rightNode;
            // 将已经处理的两棵二叉树移除
            node.remove(leftNode);
            node.remove(rightNode);
            // 把生成的新二叉树加入到NodeList中去
            node.add(parent);
        }
        // node最后的节点就是赫夫曼树根节点
        return node.get(0);
    }

    // 编写一个方法，将字符串对应的byte[]数组，通过生成的赫夫曼编码表进行处理，返回处理过后的字节数组
    static StringBuilder huffmanStr = new StringBuilder();//存储赫夫曼编码对应的字符串，在解码的时候使用
    /**
     *
     * @param bytes 原始字符串对应的byte数组
     * @param huffmanCodes 生成的赫夫曼编码
     * @return 返回处理后的byte数组，8位为一组
     * huffmanCodeBytes[0] = 10011111(补码) =>10011111-1 => 10011110(反码)=>11100001(原码)
     */
    private static byte[] zipData(byte[] bytes,Map<Byte,String> huffmanCodes){

        // 1. 利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
        StringBuilder stringBuilder = new StringBuilder();
        // 遍历bytes数组
        for (byte b:bytes){
            stringBuilder.append(huffmanCodes.get(b));
        }
        huffmanStr = stringBuilder; // 记录赫夫曼编码对应字符串
        // 字符串转成byte数组
        // 统计返回的byte[] huffmanCodeBytes长度
        // 一句代码写法： int len = (stringBuilder.length()+7)/8;
        int len;
        if(stringBuilder.length()%8==0){// 是整数
            len = stringBuilder.length()/8;
        }else{
            len = stringBuilder.length()/8+1;
        }
        // 创建存储压缩后的byte数组
        byte[] huffmanCodeBytes = new byte[len];
        int index = 0;// 记录byte次数
        for (int i = 0; i < stringBuilder.length(); i+=8) {// 步长为8
            String strByte;
            if(i+8>stringBuilder.length()){
                // 长度不够8位
                strByte = stringBuilder.substring(i);
            }else{
                // 每次取8位
                strByte = stringBuilder.substring(i,i+8);
            }
            // 将strByte，转成byte数组，放入huffmanCodeBytes
            huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2); // radix 进制
            index++;
        }
        return huffmanCodeBytes;
    }
    // 生成赫夫曼树对应的赫夫曼编码
    // 1. 将赫夫曼编码表存放在Map<Byte,String>
    static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
    // 2. 在生成赫夫曼编码表时，需要去拼接路径，定义StringBuilder存储叶子节点的路径
    static StringBuilder stringBuilder = new StringBuilder();
    // 重载getCodes
    private static Map<Byte,String> getCodes(Node root){
        if(root==null){
            return null;
        }
        // 处理root左子树
        getCodes(root.left,"0",stringBuilder);
        // 处理root右子树
        getCodes(root.right,"1",stringBuilder);
        return huffmanCodes;
    }
    /**
     *
     * @param node 节点
     * @param code  路径
     * @param stringBuilder 拼接叶子节点路径
     */
    private static void getCodes(Node node, String code, StringBuilder stringBuilder){
        StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
        // 将传入的code加入stringBuilder1
        stringBuilder1.append(code);
        if(node!=null){// 如果node为空，不处理
            // 判断当前node是否为叶子节点
            if(node.data == null){
                // 非叶子节点,递归处理
                // 向左递归,我们规定向左为"0"
                getCodes(node.left,"0",stringBuilder1);
                // 向右递归,,我们规定向右为"1"
                getCodes(node.right,"1",stringBuilder1);
            }else{
                // 是叶子节点
                huffmanCodes.put(node.data,stringBuilder1.toString());
            }
        }
    }

    // 前序遍历
    private static void preOrder(Node root){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("赫夫曼树为空");
        }
    }
}
// 创建Node，带数据和权值
class Node implements Comparable<Node>{
    Byte data; // 存放数据本身,比如' ' =>32 ,通过ascii编码来存放
    int weight; // 权值，表示字符出现的次数
    Node left;
    Node right;
    // 构造器
    public Node(Byte data, int weight) {
        this.data = data;
        this.weight = weight;
    }

    @Override
    public int compareTo(Node o) {
        return this.weight-o.weight;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                ", weight=" + weight +
                '}';
    }
    // 前序遍历
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

运行结果

文件压缩完毕！
文件解压完毕！

Process finished with exit code 0

文件解压后，大小仍然为216KB，没有损失。

赫夫曼编码注意事项

如果文件本身就是经过压缩处理的，那么使用赫夫曼编码再压缩效率不会有明显变化，例如：视频，ppt等；
赫夫曼编码是按照字节来处理的，因此可以处理所有的文件(如二进制文件，文本文件等)；
如果一个文件中的内容，重复数据不多，压缩效果也不会很明显；